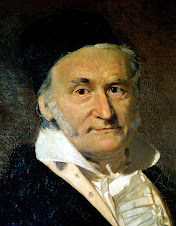Egyptian mathematics refers to mathematics written in the Egyptian language. From the Hellenistic period, Greek replaced Egyptian as the written language of Egyptian scholars. Mathematical study in Egypt later continued under the Arab Empire as part of Islamic mathematics, when Arabic became the written language of Egyptian scholars.
The most extensive Egyptian mathematical text is the Rhind papyrus (sometimes also called the Ahmes Papyrus after its author), dated to c. 1650 BC but likely a copy of an older document from the Middle Kingdom of about 2000-1800 BC.[23] It is an instruction manual for students in arithmetic and geometry. In addition to giving area formulas and methods for multiplication, division and working with unit fractions, it also contains evidence of other mathematical knowledge,[24] including composite and prime numbers; arithmetic, geometric and harmonic means; and simplistic understandings of both the Sieve of Eratosthenes and perfect number theory (namely, that of the number 6).[25] It also shows how to solve first order linear equations[26] as well as arithmetic and geometric series.[27]
Another significant Egyptian mathematical text is the Moscow papyrus, also from the Middle Kingdom period, dated to c. 1890 BC.[28] It consists of what are today called word problems or story problems, which were apparently intended as entertainment. One problem is considered to be of particular importance because it gives a method for finding the volume of a frustum: "If you are told: A truncated pyramid of 6 for the vertical height by 4 on the base by 2 on the top. You are to square this 4, result 16. You are to double 4, result 8. You are to square 2, result 4. You are to add the 16, the 8, and the 4, result 28. You are to take one third of 6, result 2. You are to take 28 twice, result 56. See, it is 56. You will find it right."
Finally, the Berlin papyrus (c. 1300 BC[29]) shows that ancient Egyptians could solve a second-order algebraic equation.[30]
Welcome; to the World of M@D M@ThS! We will show you how insanely AWESOME and USEFUL numbers can be...
Monday, 19 March 2012
Sunday, 18 March 2012
Saturday, 17 March 2012
Friday, 16 March 2012
TOP 10 GREATEST MATHEMATICIANS
Often called the language of the universe, mathematics is fundamental to our understanding of the world and, as such, is vitally important in a modern society such as ours. Everywhere you look it is likely mathematics has made an impact, from the faucet in your kitchen to the satellite that beams your television programs to your home. As such, great mathematicians are undoubtedly going to rise above the rest and have their name embedded within history.
1
Leonhard Euler
If Gauss is the Prince, Euler is the King. Living from 1707 to 1783, he is regarded as the greatest mathematician to have ever walked this planet. It is said that all mathematical formulas are named after the next person after Euler to discover them. In his day he was ground breaking and on par with Einstein in genius. His primary (if that’s possible) contribution to the field is with the introduction of mathematical notation including the concept of a function (and how it is written as f(x)), shorthand trigonometric functions, the ‘e’ for the base of the natural logarithm (The Euler Constant), the Greek letter Sigma for summation and the letter ‘/i’ for imaginary units, as well as the symbol pi for the ratio of a circles circumference to its diameter. All of which play a huge bearing on modern mathematics, from the every day to the incredibly complex.
As well as this, he also solved the Seven Bridges of Koenigsberg problem in graph theory, found the Euler Characteristic for connecting the number of vertices, edges and faces of an object, and (dis)proved many well known theories, too many to list. Furthermore, he continued to develop calculus, topology, number theory, analysis and graph theory as well as much, much more – and ultimately he paved the way for modern mathematics and all its revelations. It is probably no coincidence that industry and technological developments rapidly increased around this time.
2
Carl Friedrich Gauss
Child prodigy Gauss, the ‘Prince of Mathematics’, made his first major discovery whilst still a teenager, and wrote the incredible Disquisitiones Arithmeticae, his magnum opus, by the time he was 21. Many know Gauss for his outstanding mental ability – quoted to have added the numbers 1 to 100 within seconds whilst attending primary school (with the aid of a clever trick). The local Duke, recognizing his talent, sent him to Collegium Carolinum before he left for Gottingen (at the time it was the most prestigious mathematical university in the world, with many of the best attending). After graduating in 1798 (at the age of 22), he began to make several important contributions in major areas of mathematics, most notably number theory (especially on Prime numbers). He went on to prove the fundamental theorem of algebra, and introduced the Gaussian gravitational constant in physics, as well as much more – all this before he was 24! Needless to say, he continued his work up until his death at the age of 77, and had made major advances in the field which have echoed down through time.
3
G. F. Bernhard Riemann
Bernhard Riemann, born to a poor family in 1826, would rise to become one of the worlds prominent mathematicians in the 19th Century. The list of contributions to geometry are large, and he has a wide range of theorems bearing his name. To name just a few: Riemannian Geometry, Riemannian Surfaces and the Riemann Integral. However, he is perhaps most famous (or infamous) for his legendarily difficult Riemann Hypothesis; an extremely complex problem on the matter of the distributions of prime numbers. Largely ignored for the first 50 years following its appearance, due to few other mathematicians actually understanding his work at the time, it has quickly risen to become one of the greatest open questions in modern science, baffling and confounding even the greatest mathematicians. Although progress has been made, its has been incredibly slow. However, a prize of $1 million has been offered from the Clay Maths Institute for a proof, and one would almost undoubtedly receive a Fields medal if under 40 (The Nobel prize of mathematics). The fallout from such a proof is hypothesized to be large: Major encryption systems are thought to be breakable with such a proof, and all that rely on them would collapse. As well as this, a proof of the hypothesis is expected to use ‘new mathematics’. It would seem that, even in death, Riemann’s work may still pave the way for new contributions to the field, just as he did in life.
4
Euclid
Living around 300BC, he is considered the Father of Geometry and his magnum opus: Elements, is one the greatest mathematical works in history, with its being in use in education up until the 20th century. Unfortunately, very little is known about his life, and what exists was written long after his presumed death. Nonetheless, Euclid is credited with the instruction of the rigorous, logical proof for theorems and conjectures. Such a framework is still used to this day, and thus, arguably, he has had the greatest influence of all mathematicians on this list. Alongside his Elements were five other surviving works, thought to have been written by him, all generally on the topic of Geometry or Number theory. There are also another five works that have, sadly, been lost throughout history.
5
René Descartes
French Philosopher, Physicist and Mathematician Rene Descartes is best known for his ‘Cogito Ergo Sum’ philosophy. Despite this, the Frenchman, who lived 1596 to 1650, made ground breaking contributions to mathematics. Alongside Newton and Leibniz, Descartes helped provide the foundations of modern calculus (which Newton and Leibniz later built upon), which in itself had great bearing on the modern day field. Alongside this, and perhaps more familiar to the reader, is his development of Cartesian Geometry, known to most as the standard graph (Square grid lines, x and y axis, etc.) and its use of algebra to describe the various locations on such. Before this most geometers used plain paper (or another material or surface) to preform their art. Previously, such distances had to be measured literally, or scaled. With the introduction of Cartesian Geometry this changed dramatically, points could now be expressed as points on a graph, and as such, graphs could be drawn to any scale, also these points did not necessarily have to be numbers. The final contribution to the field was his introduction of superscripts within algebra to express powers. And thus, like many others in this list, contributed to the development of modern mathematical notation.
6
Alan Turing
Computer Scientist and Cryptanalyst Alan Turing is regarded my many, if not most, to be one of the greatest minds of the 20th Century. Having worked in the Government Code and Cypher School in Britain during the second world war, he made significant discoveries and created ground breaking methods of code breaking that would eventually aid in cracking the German Enigma Encryptions. Undoubtedly affecting the outcome of the war, or at least the time-scale.
After the end of the war he invested his time in computing. Having come up with idea of a computing style machine before the war, he is considered one of the first true computer scientists. Furthermore, he wrote a range of brilliant papers on the subject of computing that are still relevant today, notably on Artificial Intelligence, on which he developed the Turing test which is still used to evaluate a computers ‘intelligence’. Remarkably, he began in 1948 working with D. G. Champernowne, an undergraduate acquaintance on a computer chess program for a machine not yet in existence. He would play the ‘part’ of the machine in testing such programs.
7
Leonardo Pisano Blgollo
Blgollo, also known as Leonardo Fibonacci, is perhaps one of the middle ages greatest mathematicians. Living from 1170 to 1250, he is best known for introducing the infamous Fibonacci Series to the western world. Although known to Indian mathematicians since approximately 200 BC, it was, nonetheless, a truly insightful sequence, appearing in biological systems frequently. In addition, from this Fibonacci also contributed greatly to the introduction of the Arabic numbering system. Something he is often forgotten for.
Haven spent a large portion of his childhood within North Africa he learned the Arabic numbering system, and upon realizing it was far simpler and more efficient then the bulky Roman numerals, decided to travel the Arab world learning from the leading mathematicians of the day. Upon returning to Italy in 1202, he published his Liber Abaci, whereupon the Arabic numbers were introduced and applied to many world situations to further advocate their use. As a result of his work the system was gradually adopted and today he is considered a major player in the development of modern mathematics.
8
Isaac Newton and Wilhelm Leibniz
I have placed these two together as they are both often given the honor of being the ‘inventor’ of modern infinitesimal calculus, and as such have both made monolithic contributions to the field. To start, Leibniz is often given the credit for introducing modern standard notation, notably the integral sign. He made large contributions to the field of Topology. Whereas all round genius Isaac Newton has, because of the grand scientific epic Principia, generally become the primary man hailed by most to be the actual inventor of calculus. Nonetheless, what can be said is that both men made considerable vast contributions in their own manner.
9
Andrew Wiles
The only currently living mathematician on this list, Andrew Wiles is most well known for his proof of Fermat’s Last Theorem: That no positive integers, a, b and c can satisfy the equation a^n+b^n=c^n For n greater then 2. (If n=2 it is the Pythagoras Formula). Although the contributions to math are not, perhaps, as grand as other on this list, he did ‘invent’ large portions of new mathematics for his proof of the theorem. Besides, his dedication is often admired by most, as he quite literally shut himself away for 7 years to formulate a solution. When it was found that the solution contained an error, he returned to solitude for a further year before the solution was accepted. To put in perspective how ground breaking and new the math was, it had been said that you could count the number of mathematicians in the world on one hand who, at the time, could understand and validate his proof. Nonetheless, the effects of such are likely to only increase as time passes (and more and more people can understand it).
10
Pythagoras of Samos
Greek Mathematician Pythagoras is considered by some to be one of the first great mathematicians. Living around 570 to 495 BC, in modern day Greece, he is known to have founded the Pythagorean cult, who were noted by Aristotle to be one of the first groups to actively study and advance mathematics. He is also commonly credited with the Pythagorean Theorem within trigonometry. However, some sources doubt that is was him who constructed the proof (Some attribute it to his students, or Baudhayana, who lived some 300 years earlier in India). Nonetheless, the effect of such, as with large portions of fundamental mathematics, is commonly felt today, with the theorem playing a large part in modern measurements and technological equipment, as well as being the base of a large portion of other areas and theorems in mathematics. But, unlike most ancient theories, it played a bearing on the development of geometry, as well as opening the door to the study of mathematics as a worthwhile endeavor. Thus, he could be called the founding father of modern mathematics.
Monday, 12 March 2012
EXCITING MATHS GAMES!
Are you guys up for the challenge? Try these games and see who gets to the highest level!
POWER LINES!
GEOMETRY!
ALGEBRA!
POWER LINES!
GEOMETRY!
ALGEBRA!
History of Mathematics
By Tharshini Devi Krishna Moorthy
¥°. The Oriental Mathematics : Practical Arithmatic and Mensuration
¡ß Characteristic of Orient Mathematics In the Nile in Africa, the Tigris and Euphrates in western Asia, the Indus and then the Ganges in south-central Asia, and the Hwang Ho and then the Yangtze in eastern Asia, there was ancient nations called the ancient 4-civilizations until 2000 B.C.
The major economic activities of the ancient nations was to manage their farmlands and to control their products. Thus,early mathematics can be said to have originated in certain areas of the ancient Orient (the world east of Greece) primarily as a practical science to assist in agriculture, engineering, and business pursuits, that is the initial emphasis of the early mathematics was on practical arithmetic and measuration.
Algebra ultimately evolved from arithmetic and the beginnings of theoretical geometry grew out of measuration.
However that in all ancient Oriental mathematics one cannot find even a single instance of what we today call a demonstration, and one cannot find the reason to get the answer so to speak 'Do it this way' then 'Get the answer'. That is many difference from ancient Greek mathematics.
Mathematics was one of the essencial parts in the ancient civilization. Today the only record is the Egypt and Babylonia's. Finally, the orient mathematics could not be developed because it was a'living mathematics'.
The Babylonians used imperishable baked clay tablets and the Egyptians used stone and papyrus, the latter fortunately being long lasting because of the unusually dry climate of the region. But the early Chinese and lndians used very perishable media like bark and bamboo. Thus, although a fair quantity of define information is now known about the science and the mathematics of ancient Babylonia and Egypt, very little is known with any degree of certainty about these studies in ancient China and India.
¡ß Babylonian Mathematics
The early Babylonians drew isosceless triangle on wet clay plates with needles. In this way, they made wedge-shaped letters. After making cuneiform the baked the plates to keep them for a long time.
These plates were excavated at the Dynasty of King Hammurabi's era, about 1600 B.C. After deciphering the wedge-shaped letters, we can know that the babylonians used very high sysytem of calculation in commerce and agriculture with the sexagesimal positional system.
Babylonian geometry is intimately related to practical mensuration. The chief feature of Babylonian geometry is algebraic character.
Babylonians already knew the solution of quadratic eguations and eguations of second degree with two unknowns and they could aiso hondle eguations of the third and fourth degree.
Thus the development of algebra guickened. We and undoubtedly owe to the ancient Babylonians our present division of the circumference of a circle into 360 equal parts.

¡ß Egyptian Mathematics
Using a kind of reed,-papyrus- Egyptians made papers. About 1650 B.C. in 'Ahmes' Papyrus' which was written Ahmes, we can see how to calculate the fraction and the superficial measure of farmland.
Ancient Egyptians say that the area of a circle is repeatedly taken as equal to that of the square of 8/9 of the diameter.
They also extracted the volume of a right cylinder and the area of a triangle but they handled only a simple equation.

Probably the earliest way of keeping a count was by some simple tally method, employing the principle of one-to-one correspondence. In keeping a count on sheep, for example, one finger per sheep could be turned under. Counts could also be maintained by making collections of pebbles or sticks, by making scratches in the dirt or on a stone, by cutting notches in a piece of wood, or by tying knots in a string.
As the way of counting, poople should learn how to mark the numbers. Each nation, therefore, used its peculiar marking of numbers.
¡Ý The Egyptian Hieroglyphic: The Egyptian hieroglyphic numeral system is based on the scale of 10

Any number is now expressed by using these symbols additively, each symbol being repeated the required number of times. Thus,
13015=1(104)+3(103)+1(10)+5=
¡ÝThe babylonian Cuneiform : This was used from 2000 to 200 B.C. and it simplied the marking of numbers using the symbol '-'(minus)

Thus, 38=40-2+
Sometime between 3000 and 2000 B.C., the ancient Baoyionians evolved a sexagesimal system employing the principle of position.
524,551 = 2(603) + 25(602) + 42(60) + 31 = 
This method is the start of positional numberal system but the babylonians had difficulties because there was no '0'(zero) until about 300 B.C. ¡ÝThe Mayan Numeral System: This Mayan Numeral System has a symbol for '0' and is based on vigesimal. This is written very simply by dots and dashes.


The reson why this rule was developed so late is there were no plenty of papers to record on (Chinese way of making papers was introduced in Europe after 12th century). They used abacus to overcome this difficulty.
Our present addition and subtraction patterns, along with the concepts of "carrying over" and "borrowing" may have originated in the processes for carrying out these operations on the abacus.
¡ÝThe Roman Numeral System: Numeral system was decimal system or quinary, the subtractive principle, in which a symbol for a smaller unit placed before a symbol for a larger unit means the difference of the two units, was used only sparingly in ancient and medieval times.
Thus,
1944=MDCCCCXXXXIIII
1994=MCMXLIV
This way disabled them from calculating multi-digits number so they used abacus. ¡ÝThe Hindu-Arabic Numeral System: 1,2,3,4,5,6,7,8,9,0
The Hindu-Arabic numeral system is named after the Hindus, who may have invented it, and after the Arabs, who transmitted it to western Europe.; The Persian mathematician al-Khowarizmi describes such a completed Hindu system used position value or 0(zero)in a book of A.D. 825.
It is not certain when this numeral system transmitted to Europe but this system was used all over the Europe about 13th century.
The dispute between the abacist and the algorist went on. Finally, the abacus disappeared in 18th century.

By virtue of the symbol of '0' the decimal system was established. And so we can use four operations more freely than ever.
¡ß Characteristic of Orient Mathematics In the Nile in Africa, the Tigris and Euphrates in western Asia, the Indus and then the Ganges in south-central Asia, and the Hwang Ho and then the Yangtze in eastern Asia, there was ancient nations called the ancient 4-civilizations until 2000 B.C.
The major economic activities of the ancient nations was to manage their farmlands and to control their products. Thus,early mathematics can be said to have originated in certain areas of the ancient Orient (the world east of Greece) primarily as a practical science to assist in agriculture, engineering, and business pursuits, that is the initial emphasis of the early mathematics was on practical arithmetic and measuration.
Algebra ultimately evolved from arithmetic and the beginnings of theoretical geometry grew out of measuration.
However that in all ancient Oriental mathematics one cannot find even a single instance of what we today call a demonstration, and one cannot find the reason to get the answer so to speak 'Do it this way' then 'Get the answer'. That is many difference from ancient Greek mathematics.
Mathematics was one of the essencial parts in the ancient civilization. Today the only record is the Egypt and Babylonia's. Finally, the orient mathematics could not be developed because it was a'living mathematics'.
The Babylonians used imperishable baked clay tablets and the Egyptians used stone and papyrus, the latter fortunately being long lasting because of the unusually dry climate of the region. But the early Chinese and lndians used very perishable media like bark and bamboo. Thus, although a fair quantity of define information is now known about the science and the mathematics of ancient Babylonia and Egypt, very little is known with any degree of certainty about these studies in ancient China and India.
¡ß Babylonian Mathematics
The early Babylonians drew isosceless triangle on wet clay plates with needles. In this way, they made wedge-shaped letters. After making cuneiform the baked the plates to keep them for a long time.
These plates were excavated at the Dynasty of King Hammurabi's era, about 1600 B.C. After deciphering the wedge-shaped letters, we can know that the babylonians used very high sysytem of calculation in commerce and agriculture with the sexagesimal positional system.
Babylonian geometry is intimately related to practical mensuration. The chief feature of Babylonian geometry is algebraic character.
Babylonians already knew the solution of quadratic eguations and eguations of second degree with two unknowns and they could aiso hondle eguations of the third and fourth degree.
Thus the development of algebra guickened. We and undoubtedly owe to the ancient Babylonians our present division of the circumference of a circle into 360 equal parts.
¡ß Egyptian Mathematics
Using a kind of reed,-papyrus- Egyptians made papers. About 1650 B.C. in 'Ahmes' Papyrus' which was written Ahmes, we can see how to calculate the fraction and the superficial measure of farmland.
Ancient Egyptians say that the area of a circle is repeatedly taken as equal to that of the square of 8/9 of the diameter.
They also extracted the volume of a right cylinder and the area of a triangle but they handled only a simple equation.
Probably the earliest way of keeping a count was by some simple tally method, employing the principle of one-to-one correspondence. In keeping a count on sheep, for example, one finger per sheep could be turned under. Counts could also be maintained by making collections of pebbles or sticks, by making scratches in the dirt or on a stone, by cutting notches in a piece of wood, or by tying knots in a string.
As the way of counting, poople should learn how to mark the numbers. Each nation, therefore, used its peculiar marking of numbers.
¡Ý The Egyptian Hieroglyphic: The Egyptian hieroglyphic numeral system is based on the scale of 10
Any number is now expressed by using these symbols additively, each symbol being repeated the required number of times. Thus,
Sometime between 3000 and 2000 B.C., the ancient Baoyionians evolved a sexagesimal system employing the principle of position.
The reson why this rule was developed so late is there were no plenty of papers to record on (Chinese way of making papers was introduced in Europe after 12th century). They used abacus to overcome this difficulty.
Our present addition and subtraction patterns, along with the concepts of "carrying over" and "borrowing" may have originated in the processes for carrying out these operations on the abacus.
¡ÝThe Roman Numeral System: Numeral system was decimal system or quinary, the subtractive principle, in which a symbol for a smaller unit placed before a symbol for a larger unit means the difference of the two units, was used only sparingly in ancient and medieval times.
| 1 | 5 | 10 | 50 | 10©÷ | 500 | 10©ø |
| I | V | X | L | C | D | M |
1994=MCMXLIV
This way disabled them from calculating multi-digits number so they used abacus. ¡ÝThe Hindu-Arabic Numeral System: 1,2,3,4,5,6,7,8,9,0
The Hindu-Arabic numeral system is named after the Hindus, who may have invented it, and after the Arabs, who transmitted it to western Europe.; The Persian mathematician al-Khowarizmi describes such a completed Hindu system used position value or 0(zero)in a book of A.D. 825.
It is not certain when this numeral system transmitted to Europe but this system was used all over the Europe about 13th century.
The dispute between the abacist and the algorist went on. Finally, the abacus disappeared in 18th century.
By virtue of the symbol of '0' the decimal system was established. And so we can use four operations more freely than ever.
fascinating facts of mathemathics
- The word "MATHEMATICS" comes from the Greek μάθημα (máthema) which means "science, knowledge, or learning"; μαθηματικός (mathematikós) means "fond of learning".
- The word "FRACTION" derives from the Latin " fractio - to break".
- GEOMETRY(Ancient Greek: γεωμετρία; geo = earth, metria = measure) is a part of mathematics.
- "ALGEBRA" comes Arabic word (al-jabr, literally, restoration)
- There are just four numbers (after 1) which are the sums of the cubes of their digits:
153 = 1^3 + 5^3 + 3^3
370 = 3^3 + 7^3 + 0^3
371 = 3^3 + 7^3 + 1^3
407 = 4^3 + 0^3 + 7^3
- 111,111,111 multiplied by 111,111,111 equals12,345,678,987,654,321.
- Among all shapes with the same area circle has the shortest perimeter.
- For every object there is a distance at which it looks its best.
- The Five Most Important Numbers in Mathematics in One Equation :
e^i*pi + 1 = 0
Sunday, 11 March 2012
Saturday, 10 March 2012
10 reasons to love numbers ! --> Silly but VERY true
1 - NO NEED to memorize silly historical dates!
2 - DON'T NEED to be a good public speaker OR a stand up comedian to do it !
3 - ANSWERING math questions RARELY requires you to write a five paragraph essay or riming.
4 - Mathematic is a UNIVERSAL LANGUAGE !
5 - NO COMPLICATED verb Conjunctions
6 - Recipe ONLY involves MATHEMATICAL MEASUREMENTS
7 - Its practical ! you can apply it in your almost DAILY LIFE.
8 -You don't have to memorize things during a test, just solve PROBLEMS
9 -YOU are ALLOWED to use a calculator
10 - People THINK you're SMART if you're good at it!!!
Source - Google.com
By : Alina Mf
2 - DON'T NEED to be a good public speaker OR a stand up comedian to do it !
3 - ANSWERING math questions RARELY requires you to write a five paragraph essay or riming.
4 - Mathematic is a UNIVERSAL LANGUAGE !
5 - NO COMPLICATED verb Conjunctions
6 - Recipe ONLY involves MATHEMATICAL MEASUREMENTS
7 - Its practical ! you can apply it in your almost DAILY LIFE.
8 -You don't have to memorize things during a test, just solve PROBLEMS
9 -YOU are ALLOWED to use a calculator
10 - People THINK you're SMART if you're good at it!!!
Source - Google.com
By : Alina Mf
Sunday, 4 March 2012
Subscribe to:
Comments (Atom)